MAST 234 Notes
Mast 234: Linear Algebra & Applications
- Maple software
- Maple commands
Linear Algebra & Applications
Remember
with(LinearAlgebra)
Lecture 1
review of systems of linear equations
- any
row-equivalentmatrix has one and only one reduced row echelon form A := Matrix(3,3,[1,2,3,4,5,6,7,8,0])3x3 MatrixA := RowOperation(A1, [1,2], 1/c)ReducedRowEchelonForm(A)- can use vectors together
ReducedRowEchelonForm(<u|v|w|x|y|z>);to check if it is in the span
- can use vectors together
GaussianElimination(A)GenerateMatrix([eq1,eq2,eq3], X)- check the point(1,3,2) is a solution of the equations
subs([x1=1,x2=3,x3=2],[eq1,eq2,eq3,eq4])
C1 = Column(A,1)orC1,C2,C3 = Column(A, 1..3)ReducedRowEchelonForm(<A|b>)
Lecture 2
vectors, matrices, spans
- vectors:
- Column:
X := <x1,x2,x3>,Vector([y1,y2,y3]) - row:
Vector[row]([1,c,3])
- Column:
- Matrix equations as Linear combination of vectors
AX = b = x1C1 + x2C2 + X3C3(Linear combination)ReducedRowEchelonForm(<c1|c2|b>)get x1,x2 if has solution, then b = c1x1 + c2x2, checkAX=b- check AX=b:
x1*Column(A,1)+x2*Column(A,2)+x3*Column(A,3) = b;
- 3 types of matrix
no solution->inconsistent, such as0 = 1after useRREF(ReducedRowEchelonForm)unique solution->consistentinfinite solution->consistent, such as0 = 0of x2 then x2 is afree variable.- use
ReducedRowEchelonFormandGaussianEliminationto check if the system is consistent or not and solutions.
spansof vector sets- Span{C1,C2…Cn} = {a1C1 + a2C2 +… + anCn}
- eg. span(u,v), u=(1,0), v=(0,1) is xu+yv=(x,y): an entire space R^2!!!
- can use vectors together
ReducedRowEchelonForm(<u|v|w|x|y|z>);to check if it is in the span
Transpose function:Transpose(Matrix)`- M = <<1,2,3>|<4,5,6>> : 3X2
- M^T = <<1,4>|<2,5>|<3,6>> : 2X3
- Matrix multiplication is use
dot .notstar *differentlyA . X = v;
example:

Lecture 3
Linear dependence of vectors
Homogeneous System, Kernel, Rank
linearly dependent/independent
- linearly dependent: of there exists a
non-trivial(non all zero) solution to the vector equationc1u1 + c2u2 +...+ cnun = 0 - linearly independent: only the trivial solution (c1=c2=…=cn=0)
Homogeneous system of equations:
- a system of linear equations
AX=0 - A is a
m X nmatrix - 0 vector is an m-dimensinal
zero-vector - any homogeneous system is
always consistent, since it has at least one solution (trivial solution)- the column of vectors of matrix A form a
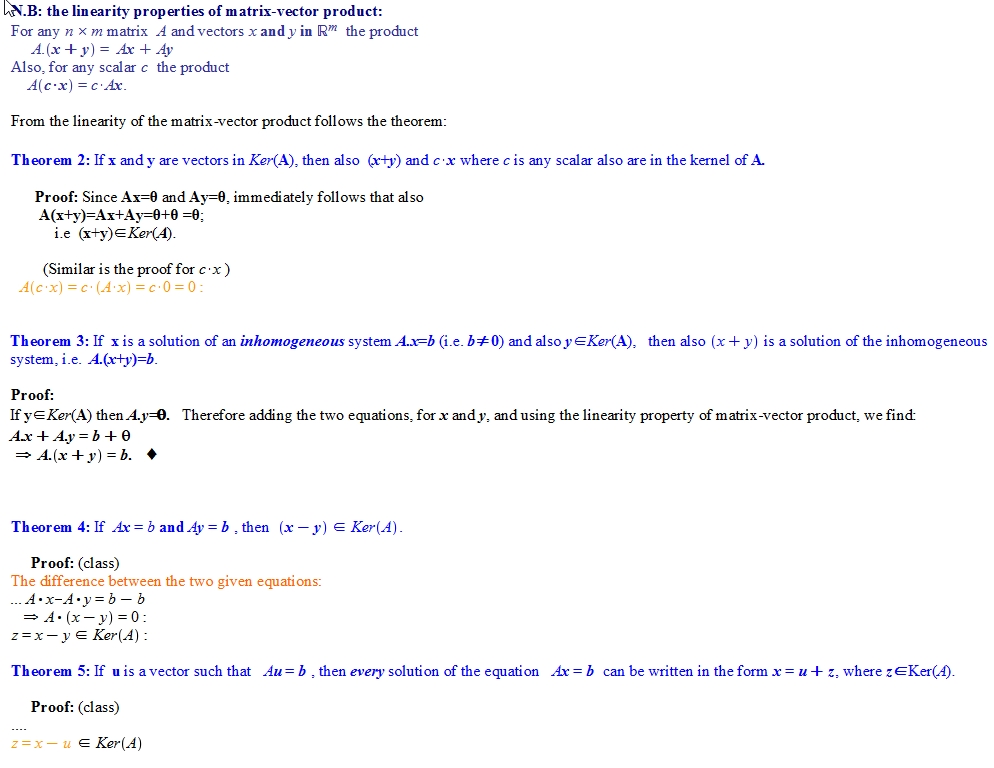
linearly dependentif the linear system AX=0 has afree variable. Otherwise, the column vectors of A arelinearly independent - Kernel (Null space) of the matrix A
- the column of vectors of matrix A form a
Ker(A) = {X: A.X=0} = Null(A)- Ker(A) is
never an empty setsince it contains at least the zero vector 0 !!!- Example:

- Theorems:

- Exercise:

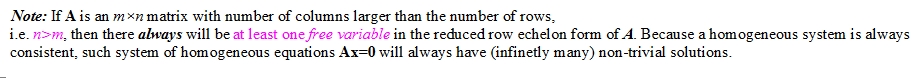
- Example:
Linear dependence/independence of Vectors
- Exercise:

- example2:

- Example 3:

- Theorems:

- Theorems:
Rank
- The
rankof a matrix A is thenumber of non-zero rowsin itsrow echelon form, r = Rank(A) - Example:
- Exercise:

- 如果含有parameter,要使用
GaussianElimination()
- 需要check,当u=0时候,在之前的题目里已经知道Rank(B)=3

- Exercise:
- some important Theorems:

MAST 234 Notes