COMP 367 notes

COMP 367: Techniques in Symbolic Computation

• Maple Software
• Maple commands

Lecture 1

• Division Theorem:

  • b = q*a + r, 0<=r<a, q>=0 and a, b>0
  • a is divisor, b is divident, q is quotient, r is remainder
  • a divides b is a|b , also called a is a divisor of b or a is a factor of b

• GCD (greatest common divisor)

  • gcd(30,45)

• common multiple

  • 45 is a common multiple of 5 and 3.
  • c = ab, (45 is c, 5,3=a,b)

• prime: only two divisors: 1 and itself

  • ithprime(1003)
  • seq(ithprime(i),i=1..10)

• coprime: if (a,b) = 1

  • (lecture 2) ar + bs = 1

• Euclid’s Algorithm:

  • get quotient: irem(365,121,'q') or iquo(365,121)
  • use list to calculate:( order is not important!!! )
    • EA := l::list->[l[2],l[1]-l[2]*iquo(l[1],l[2])];
    • l1 := EA([aaa, bbb])
    • l2 := EA(l1)
  • use do-loop:

    l_n := EA([111,2222]);
    do
       l_n := EA(l_n)
    until l_n[2] = 0:
    l_n;

• need check with gcd(a,b)

Lecture 2

• Bezout’s Identity:

  • if (a, b)=d then d = at + bs for some integers t and s
    

• Extended Euclid’s Algorithm

  • r = xa + yb
  • find row1 and row2
    • row1 := [y, 0, 1];
    • row2 := [x, 1, 0];
  • find 3rd and etc.
    • row3 := row1 - iquo(row1[1],row2[1])*row2
    • continue to other lines
    • another function: EEA := (l1,l2)->l1-l2*iquo(l1[1],l2[2]);
      • can use do-loop:

        k := 0:
        m := 2:
        do
           k:=k+1:
           m:=m+1:
           row||m := EEA(row||k, row||(k+1));
           print(row||m)
        until row||m[1]=0:

  • EEA := Matrix(4,3,[row1,row2,row3...]) until the remainder of row is 0.
  • Corollary 8: if a divides bc and (a,b)=1, then a divides c

• Diophantine Equations:

  • a*x + b*y = c is a linear Diophantine Equation
  • question is find a solution of the equation
  • use EEA function and steps above
  • For General solution
    • when row is like [0, z, w], then x0=zk, y0=wk where k is any integer.
    • z need positive(+), if z is negative(-), exchange z and w such as [0, -9, 2]-> z=9, w=-2
    • 1 = 2x+ y to find = 22, need to multiple 22, then 22 = (2*22)x + (22)y
    • the general solution is x=(2*22) + z , y = 22 + w

• Factorization:

  • Induction Theorem: Let P(n) be a statement that is defined for any integer n>= n0;
    • (1) P(n0) is true
    • (2) if P(n) is true for some n>=n0, then P(n+1) is also true.
  • ifactor(45); such as (3)^2(5)

• Least Common Multiple (LCM):

  • Proposition: [a,b]=(a*b)/(a,b)
  • lcm(210,126); result is 630.

Lecture 3

Congruences

• Congruence Modulo m
  
  • 143 mod 14, -5 mod 10
  • evalb(16 mod 5 = 31 mod 5) is true
• properties:
  
• Proposition:
  
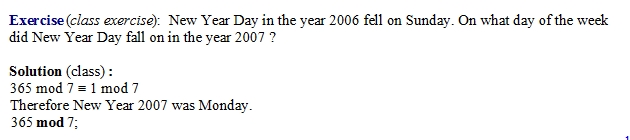
  • ex:
    

Linear Congruencies and Bezout’s Identity

• ex2:
  
• ex3:
  
• Proposition 19:
  
  • ex:
    
• Systems of Congruences:
  

Basic properties of congruences:

• properties:
  
  • ex:
    
• Proposition:
  
  • Application of the exponentiation: